Descubre los Secretos Matemáticos detrás de la IA

Guía Esencial de matemáticas básicas para la IA para No Expertos

En el dinámico mundo de la tecnología, la Inteligencia Artificial (IA) se ha convertido en el motor de innovación de numerosas industrias. Pero, ¿qué hay realmente detrás de esta revolución tecnológica? En este post, exploraremos en profundidad los principios matemáticos y estadísticos fundamentales que impulsan la Ciencia de Datos y la IA.

La Trinidad de la IA: Computación, Matemáticas y Conocimiento del Dominio

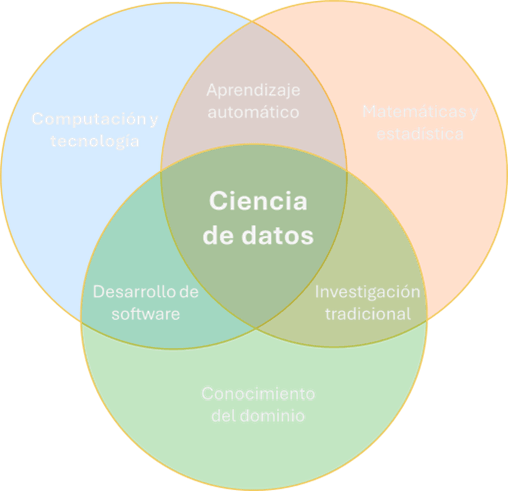
La IA y la Ciencia de Datos emergen de la intersección de tres áreas clave: la Ciencia de la Computación, las Matemáticas y Estadística, y el Conocimiento del Dominio o Negocio. Esta trinidad forma la base sobre la cual se construyen las aplicaciones más avanzadas de IA que vemos hoy en día.

La Ciencia de la Computación proporciona los algoritmos y la infraestructura tecnológica necesaria para procesar grandes volúmenes de datos de manera eficiente. Los conceptos clave de esta disciplina serían: estructuras de datos, complejidad algorítmica y arquitectura de sistemas. Por ejemplo, un algoritmo de búsqueda binaria puede hacer que encontrar un elemento en una lista ordenada sea exponencialmente más rápido que una búsqueda lineal, lo cual es crucial cuando se trabaja con conjuntos de datos masivos en aplicaciones de IA.

Las Matemáticas y la Estadística ofrecen las herramientas para analizar y modelar datos, permitiendo extraer información significativa y hacer predicciones precisas. Esta área abarca desde el álgebra lineal y el cálculo hasta la teoría de la probabilidad y la estadística inferencial. Un ejemplo concreto es el análisis de componentes principales (PCA), una técnica que utiliza álgebra lineal para reducir la dimensionalidad de los datos, permitiendo visualizar y procesar información compleja de manera más eficiente.

El Conocimiento del Dominio o Negocio aporta el contexto y la relevancia práctica necesarios para que las soluciones de IA sean realmente útiles en el mundo real. Esto incluye la comprensión profunda del sector en el que se aplica la IA, las regulaciones pertinentes y los objetivos específicos del negocio. Por ejemplo, en el sector financiero, el conocimiento detallado de las regulaciones bancarias es crucial para desarrollar modelos de detección de fraude que sean tanto efectivos como conformes con la ley.

La verdadera magia de la IA ocurre cuando estas tres áreas se combinan de manera sinérgica. Tomemos como ejemplo un sistema de recomendación para una plataforma de comercio electrónico. Este sistema utiliza algoritmos eficientes de la Ciencia de la Computación para procesar rápidamente grandes volúmenes de datos de usuarios. Luego, aplica modelos estadísticos avanzados para identificar patrones complejos en el comportamiento de compra. Finalmente, incorpora conocimiento profundo sobre tendencias de mercado y comportamiento del consumidor para hacer recomendaciones que sean no solo precisas, sino también relevantes y oportunas para cada usuario individual. Incluso aunque optes por utilizar herramientas no-code, necesitarás un conocimiento mínimo sobre estas tres disciplinas.

Regresión Lineal: Comprendiendo la Relación entre Ventas y Precios

Uno de los conceptos fundamentales en estadística y aprendizaje automático es la regresión lineal. Esta técnica nos permite entender y modelar la relación entre variables, lo cual es crucial en muchas aplicaciones de IA. Para ilustrar este concepto, imaginemos que eres el CEO de “TechMart”, una tienda de electrónica, y quieres entender cómo el precio de tus productos afecta a las ventas. Has recopilado datos de ventas de un modelo específico de smartphone durante los últimos 30 días, variando ligeramente su precio cada día.

Al analizar estos datos mediante regresión lineal, obtenemos un gráfico de dispersión que muestra la relación entre el precio (eje horizontal) y las unidades vendidas (eje vertical). Los puntos en el gráfico representan las observaciones reales. La recta que atraviesa estos puntos representa nuestro modelo de regresión lineal. Por tanto, un modelo no es más que una herramienta matemática que resulta de utilidad para una tarea concreta, en nuestro caso, describir cómo se relacionan el número de unidades vendidas de un cierto smartphone con su precio de venta.

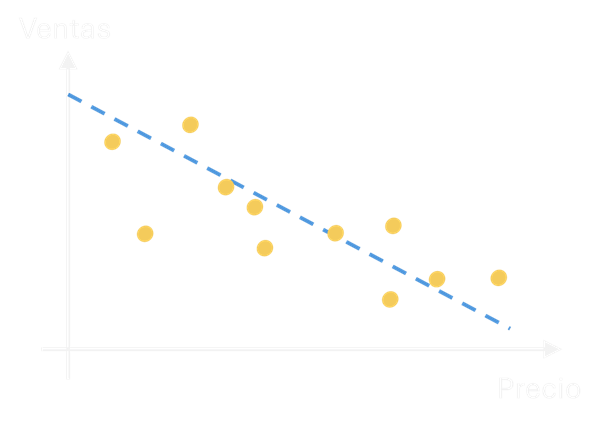
En nuestro caso, el modelo es una simple recta. Esta línea de regresión es una simplificación de la realidad que nos permite hacer predicciones. Su ecuación toma la forma de “Unidades Vendidas = m * Precio + b”, donde ‘m’ es la pendiente (que indica cómo cambian las ventas por cada unidad de cambio en el precio) y ‘b’ es el término independiente (el punto donde la línea cruza el eje Y).

Por ejemplo, si nuestra ecuación fuera “Unidades Vendidas = -0.2 * Precio + 200”, esto nos indicaría que por cada euro que aumenta el precio, esperamos vender 0.2 unidades menos. El término independiente de 200 sugiere que si el precio fuera 0€ (una situación hipotética), esperaríamos vender 200 unidades. Sin embargo, es importante notar que extrapolar de esta manera puede no ser realista en la práctica. Esta es una de las primeras lecciones que tenemos que aprender cuando tratemos con modelos matemáticos: antes de usarlos, debemos comprender su aplicabilidad.

El modelo anterior nos permitiría hacer predicciones sencillas que nos permitiesen comprender escenarios hipotéticos. Por ejemplo, si quisiéramos predecir las ventas con un precio de 650€, simplemente sustituiríamos este valor en nuestra ecuación: Unidades Vendidas = -0.2 * 650 + 200 = 70 unidades.

La potencia de este modelo radica en su capacidad para simplificar relaciones complejas y hacer predicciones basadas en datos. Es más eficiente que consultar constantemente toda la base de datos, nos da una visión general de la tendencia, y nos permite hacer predicciones para precios que no hemos probado en la realidad.

Un buen modelo de regresión lineal es aquel que hace pequeño el error, es decir, la diferencia entre las predicciones del modelo y los datos reales. Visualmente, esto se traduce en que cuanto más cerca estén los puntos de la línea de regresión, mejor será nuestro modelo. Para lograr esto, la técnica más habitual es la de “minimizar el error cuadrático medio”, donde calculamos la diferencia entre cada valor real y el predicho por el modelo (los llamados “residuos”), elevamos al cuadrado estas diferencias, las sumamos, y buscamos la línea que minimiza esta suma.

En la práctica, podrías usar este tipo de modelo para predecir ventas a diferentes precios, encontrar el precio que maximiza los ingresos, o entender la sensibilidad de tus clientes al precio. Sin embargo, es importante recordar que la relación entre precio y ventas en el mundo real puede ser más compleja, involucrando factores adicionales como estacionalidad, competencia, o características específicas del producto. Modelos más avanzados en IA pueden capturar estas complejidades, pero a nivel conceptual funcionan igual que el modelo de regresión lineal.

La Regla de Bayes: Una Revolución en el Pensamiento Probabilístico

La Regla de Bayes, nombrada en honor al reverendo Thomas Bayes (1701-1761), es uno de los pilares de la probabilidad y la estadística moderna. Aunque Bayes nunca publicó su trabajo en vida, sus ideas fueron desarrolladas y publicadas póstumamente por Richard Price en 1763.

La Regla de Bayes: Fórmula y Explicación

La Regla de Bayes se expresa matemáticamente como:

P(A|B) = (P(B|A) × P(A)) / P(B)

Donde:

• P(A|B) es la probabilidad de A dado B (probabilidad posterior)
• P(B|A) es la probabilidad de B dado A (verosimilitud)
• P(A) es la probabilidad de A (probabilidad previa)
• P(B) es la probabilidad de B (evidencia)

Pero, ¿qué significa esto en términos prácticos?

La Regla de Bayes nos permite actualizar nuestras creencias sobre la probabilidad de un evento A, dado que hemos observado un evento B. En otras palabras, nos ayuda a incorporar nueva información para mejorar nuestras estimaciones de probabilidad.

Un Ejemplo Práctico: Pruebas Médicas

Imaginemos que eres el CEO de una empresa de tecnología médica que ha desarrollado una nueva prueba para detectar una enfermedad rara. Vamos a usar la Regla de Bayes para entender la efectividad de esta prueba.

Datos:

• La enfermedad afecta al 1% de la población (P(E) = 0.01)
• La prueba tiene una sensibilidad del 95%: si una persona tiene la enfermedad, la prueba será positiva el 95% de las veces (P(T+|E) = 0.95)
• La prueba tiene una especificidad del 90%: si una persona no tiene la enfermedad, la prueba será negativa el 90% de las veces (P(T-|no E) = 0.90)

Pregunta: Si la prueba de una persona da positivo, ¿cuál es la probabilidad de que realmente tenga la enfermedad?

Aplicando la Regla de Bayes:

1. P(E|T+) = (P(T+|E) * P(E)) / P(T+)
2. P(T+) = P(T+|E) * P(E) + P(T+|no E) * P(no E) = 0.95 * 0.01 + 0.10 * 0.99 = 0.0095 + 0.099 = 0.1085
3. P(E|T+) = (0.95 * 0.01) / 0.1085 ≈ 0.0876 o 8.76%

Interpretación: Aunque la prueba dio positivo, la probabilidad de que la persona realmente tenga la enfermedad es de solo alrededor del 8.76%. Esto puede parecer contraintuitivo, pero se debe a la baja prevalencia de la enfermedad en la población general.

Importancia en IA y Aprendizaje Automático

La Regla de Bayes es fundamental en muchos algoritmos de IA y aprendizaje automático:

1. Clasificadores Bayesianos: Usados en filtros de spam, sistemas de recomendación y diagnóstico médico.
2. Redes Bayesianas: Modelan relaciones causales entre variables, útiles en sistemas expertos y toma de decisiones.
3. Inferencia Bayesiana: Permite actualizar modelos de aprendizaje automático a medida que llegan nuevos datos.
4. Optimización de Hiperparámetros: Ayuda a ajustar los parámetros de modelos complejos de aprendizaje automático.

La Regla de Bayes nos recuerda que debemos considerar tanto la evidencia que observamos como nuestro conocimiento previo al hacer inferencias. En el mundo de los big data y la IA, donde constantemente estamos actualizando nuestros modelos con nueva información, el pensamiento bayesiano es más relevante que nunca.

Probabilidad: La Ciencia de la Incertidumbre

La probabilidad es el lenguaje matemático que usamos para describir y cuantificar la incertidumbre. En el mundo de la IA y la ciencia de datos, donde a menudo trabajamos con información incompleta o ruidosa, la probabilidad es una herramienta indispensable.

Conceptos Fundamentales

1. Evento: Un resultado posible de un experimento. Ejemplo: Obtener cara al lanzar una moneda.
2. Espacio Muestral: El conjunto de todos los posibles resultados de un experimento. Ejemplo: {cara, cruz} para el lanzamiento de una moneda.
3. Probabilidad de un Evento: Un número entre 0 y 1 que describe la probabilidad de que ocurra un evento.
   1. 0 significa que el evento es imposible.
   1. 1 significa que el evento es seguro.
   1. 0.5 significa que el evento tiene un 50% de probabilidad de ocurrir.

Reglas Básicas de Probabilidad

1. Regla de la Suma: Para eventos mutuamente excluyentes A y B: P(A o B) = P(A) + P(B), o lo que es lo mismo, la probabilidad de que pase A ó B es la suma de la probabilidad de que pase A más la probabilidad de que pase B.
2. Regla del Producto: Para eventos independientes A y B: P(A y B) = P(A) * P(B), o lo que es lo mismo, la probabilidad de que pase A y B es la probabilidad de que pase A multiplicada por de la probabilidad de que pase B.
3. Regla del Complemento: Para un evento A: P(no A) = 1 – P(A), o lo que es lo mismo, la probabilidad de que no pase A uno menos la probabilidad de que pase A.

Probabilidad Condicional y Árboles de Probabilidad

La probabilidad condicional es la probabilidad de que ocurra un evento A, dado que ha ocurrido otro evento B. Se denota como P(A|B).

Veamos un ejemplo práctico usando árboles de probabilidad:

Imagina que eres el CEO de una empresa de marketing digital y estás analizando los patrones publicitarios de las empresas en tu industria:

• El 70% de las empresas usan publicidad en internet
• El 30% usan radio/televisión
• De las que usan internet:
  • El 20% utilizan publicidad en podcasts
  • El 80% utilizan publicidad en redes sociales

Podemos representar esto en un árbol de probabilidades:

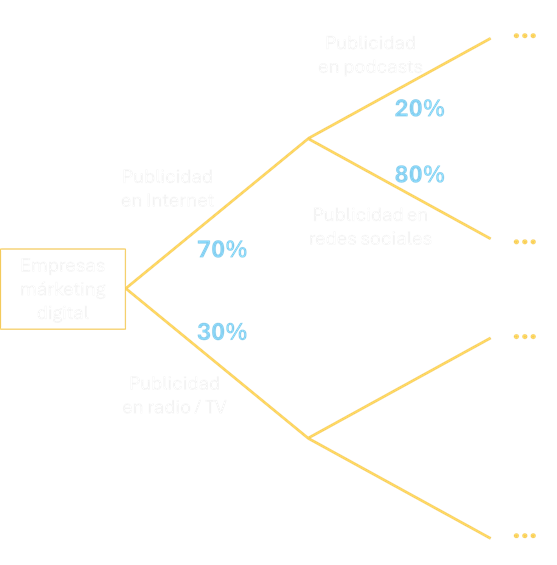
Este árbol de probabilidad nos permite visualizar y calcular varias probabilidades importantes:

1. Probabilidad Simple:
   1. P(Internet) = 70% = 0.7
   1. P(Radio/TV) = 30% = 0.3
2. Probabilidad Condicional:
   1. P(Podcasts | Internet) = 20% = 0.2
   1. P(Redes Sociales | Internet) = 80% = 0.8

Ahora, respondamos algunas preguntas utilizando este árbol:

1. ¿Cuál es la probabilidad de que una empresa use publicidad en podcasts? Respuesta: 70% * 20% = 14% Explicación: Multiplicamos la probabilidad de usar internet (70%) por la probabilidad de usar podcasts dado que usan internet (20%).
2. ¿Cuál es la probabilidad de que una empresa NO use publicidad en internet? Respuesta: 100% – 70% = 30% Explicación: Usamos la regla del complemento. La probabilidad de no usar internet es el complemento de la probabilidad de usarlo.
3. ¿Cuál es la probabilidad de que una empresa use publicidad en redes sociales? Respuesta: 70% * 80% = 56% Explicación: Multiplicamos la probabilidad de usar internet (70%) por la probabilidad de usar redes sociales dado que usan internet (80%).
4. Si sabemos que una empresa usa internet para publicidad, ¿cuál es la probabilidad de que use podcasts? Respuesta: 20% Explicación: Esta es directamente la probabilidad condicional que vemos en el árbol.

Teorema de la Probabilidad Total

El teorema de la probabilidad total nos permite calcular la probabilidad de un evento B considerando todos los posibles escenarios mutuamente excluyentes (A1, A2, …, An) que podrían llevar a B:

P(B) = P(B|A1)P(A1) + P(B|A2)P(A2) + … + P(B|An)P(An)

En nuestro ejemplo:

P(Podcasts) = P(Podcasts|Internet)P(Internet) + P(Podcasts|Radio/TV)P(Radio/TV) = 0.2 * 0.7 + 0 * 0.3 = 0.14

Notas:

• Asumimos que las empresas que usan Radio/TV no usan podcasts (P(Podcasts|Radio/TV) = 0)
• Este resultado coincide con nuestro cálculo anterior

Importancia en IA y Ciencia de Datos

La probabilidad es fundamental en IA y ciencia de datos por varias razones:

1. Manejo de la Incertidumbre: Los modelos de IA a menudo trabajan con datos ruidosos o incompletos. La probabilidad nos permite cuantificar y manejar esta incertidumbre.
2. Inferencia Estadística: Usamos probabilidad para hacer inferencias sobre poblaciones basándonos en muestras de datos.
3. Modelos Probabilísticos: Muchos algoritmos de aprendizaje automático, como los clasificadores Naive Bayes o las Redes Bayesianas, se basan directamente en la teoría de la probabilidad.
4. Toma de Decisiones: En aplicaciones como sistemas de recomendación o diagnóstico médico, la probabilidad nos ayuda a tomar decisiones óptimas bajo incertidumbre.
5. Evaluación de Modelos: Métricas como la precisión, el recall o el AUC-ROC se basan en conceptos probabilísticos.

Estadística Descriptiva: Entendiendo nuestros Datos

La estadística descriptiva nos proporciona herramientas para resumir y visualizar grandes conjuntos de datos, permitiéndonos obtener insights valiosos. Una de las herramientas más poderosas en este ámbito es el histograma.

El Histograma: Una Ventana a la Distribución de Datos

Imaginemos que eres el CEO de “InvestSmart”, una empresa de inversiones, y quieres entender el rendimiento de uno de tus fondos más populares. Has recopilado datos sobre el retorno diario de la inversión durante el último año (252 días hábiles).

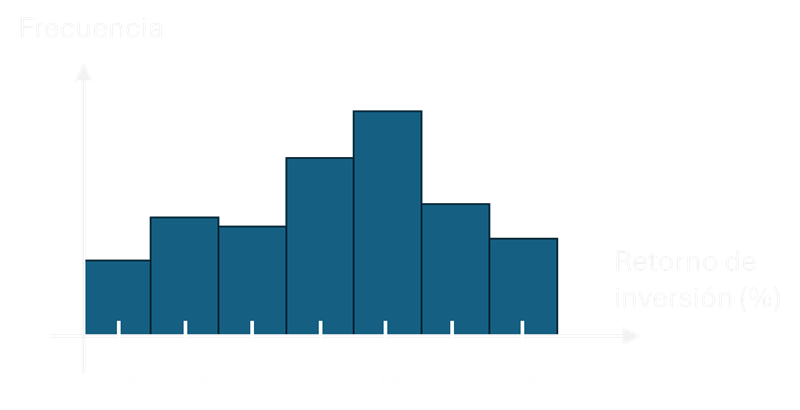
Desglosemos este histograma y los conceptos estadísticos relacionados:

1. Construcción del Histograma:
   1. Dividimos el rango de retornos en intervalos (en este caso, 20 intervalos).
   1. Contamos cuántos días caen en cada intervalo.
   1. La altura de cada barra representa la frecuencia de días en ese intervalo.
2. Interpretación:
   1. La forma del histograma nos da una idea de la distribución de los retornos.
   1. En este caso, vemos una forma aproximadamente simétrica y en forma de campana, lo que sugiere una distribución normal.
3. Media: La media es el promedio aritmético de todos los retornos. Es una medida de tendencia central. Fórmula: μ = (Σx) / n, donde x son los valores individuales y n es el número total de valores. En nuestro histograma, la media parece estar alrededor del 0.5%. Ejemplo de cálculo: Si tuviéramos solo 5 días con retornos de 0.2%, 0.5%, 0.7%, 0.4%, y 0.6%: μ = (0.2 + 0.5 + 0.7 + 0.4 + 0.6) / 5 = 0.48%
4. Mediana: La mediana es el valor central cuando ordenamos todos los retornos. En una distribución simétrica como esta, suele estar cerca de la media. Para encontrar la mediana:
   1. Ordena todos los valores de menor a mayor.
   1. Si n es impar, la mediana es el valor en la posición (n+1)/2.
   1. Si n es par, la mediana es el promedio de los dos valores centrales.
5. Moda: La moda es el valor que aparece con más frecuencia. En nuestro histograma, correspondería al intervalo con la barra más alta.
6. Varianza y Desviación Estándar: Estas medidas nos dicen cuánto se dispersan típicamente los retornos alrededor de la media. En finanzas, esto se relaciona con el concepto de “riesgo”. Vamos a explorar estos conceptos paso a paso: a) Error o Desviación: Si tomamos la media como medida de centralidad, el “error” para cada observación es su distancia desde la media. Error = x – μ, donde x es un valor individual y μ es la media. b) Promedio de Errores: Si simplemente promediáramos estos errores, siempre obtendríamos cero, ya que los errores positivos y negativos se cancelarían entre sí. c) Varianza: Para solucionar el problema de los signos, elevamos al cuadrado cada error antes de promediar. Esto nos da la varianza. Fórmula de la Varianza: σ² = Σ(x – μ)² / (n-1) Ejemplo simplificado: Retornos: 0.2%, 0.5%, 0.7%, 0.4%, 0.6% Media (μ) = 0.48% Errores al cuadrado: (0.2-0.48)² + (0.5-0.48)² + (0.7-0.48)² + (0.4-0.48)² + (0.6-0.48)² = 0.0784 + 0.0004 + 0.0484 + 0.0064 + 0.0144 Varianza = (0.0784 + 0.0004 + 0.0484 + 0.0064 + 0.0144) / (5-1) = 0.037% d) Desviación Estándar: La desviación estándar es simplemente la raíz cuadrada de la varianza. La usamos porque está en las mismas unidades que nuestros datos originales. Fórmula de la Desviación Estándar: σ = √σ² En nuestro ejemplo simplificado: σ = √0.037% ≈ 0.19% Interpretación: Una desviación estándar de 0.19% significa que, en promedio, los retornos diarios se desvían alrededor de 0.19 puntos porcentuales de la media.
7. Coeficiente de Variación de Pearson: El coeficiente de variación (CV) es una medida de dispersión relativa que nos permite comparar la variabilidad entre diferentes conjuntos de datos, incluso si tienen diferentes unidades o escalas. Fórmula: CV = (σ / μ) * 100% En nuestro ejemplo simplificado: CV = (0.19 / 0.48) * 100% ≈ 39.58% Interpretación: Un CV de 39.58% sugiere que la desviación estándar es aproximadamente el 40% del valor de la media, indicando una variabilidad relativamente alta en los retornos.

Aplicaciones en IA y Ciencia de Datos

La estadística descriptiva es fundamental en IA y ciencia de datos por varias razones:

1. Exploración de Datos: Nos ayuda a entender la naturaleza y características de nuestros datos antes de aplicar modelos más complejos.
2. Detección de Anomalías: Valores que están muy lejos de la media (varios múltiplos de la desviación estándar) pueden ser indicativos de anomalías o errores en los datos.
3. Preparación de Datos: Muchos algoritmos de aprendizaje automático asumen que los datos siguen ciertas distribuciones. Entender la distribución de nuestros datos nos ayuda a elegir y preparar los datos adecuadamente.
4. Evaluación de Modelos: Medidas como el error cuadrático medio (basado en la varianza) son comunes para evaluar el rendimiento de modelos predictivos.
5. Comunicación de Resultados: Los histogramas y las medidas de resumen son herramientas poderosas para comunicar insights de manera clara y concisa a stakeholders no técnicos.

En el mundo de la IA y el big data, donde a menudo trabajamos con conjuntos de datos masivos y complejos, la estadística descriptiva nos proporciona una base sólida para entender y comunicar las características esenciales de nuestros datos. Esta comprensión es crucial para tomar decisiones informadas, tanto en el desarrollo de modelos de IA como en la interpretación de sus resultados.

Conclusión

Los principios matemáticos y estadísticos que hemos explorado son los cimientos sobre los que se construye la moderna Ciencia de Datos e Inteligencia Artificial. Desde la regresión lineal hasta la estadística descriptiva, pasando por la probabilidad y la Regla de Bayes, estos conceptos nos proporcionan las herramientas para entender, modelar y predecir el mundo que nos rodea.

Entender estos conceptos básicos te permitirá:

1. Comunicarte más efectivamente con trabajadores técnico.
2. Tomar decisiones más informadas sobre cómo implementar soluciones de IA.
3. Interpretar y cuestionar los resultados de los modelos de manera crítica.
4. Identificar nuevas oportunidades donde la IA y la ciencia de datos puedan aportar valor a tu organización.

Recuerda, la IA no es magia, sino la aplicación sistemática de estos principios matemáticos a grandes volúmenes de datos. Con esta base, estás mejor equipado para navegar el emocionante mundo de la IA y aprovechar su potencial para impulsar la innovación y el crecimiento en tu proyecto.